Efficiency – a calculation

Since Aptera’s main promise is its groundbreaking efficiency, in this blog I will try to explain with some basic calculations where Aptera gets its efficiency from. The energy use of any electric vehicle revolves around several types of losses that occur:

• Air resistance: the power needed to force the air molecules around the car.
• Rolling resistance: the power consumed by the tires and road.
• Mechanical drivetrain losses
• Friction losses when applying the brakes
• Electrical losses
• Losses for auxillary equipment such as audio and heating

Depending on what type of driving you’re doing, the ratio between all losses changes. For instance, when driving at a constant speed on a highway with little traffic, the losses of the brakes becomes zero and the air resistance becomes dominant. The exact opposite occurs in heavy traffic with a lot of stop-and-go movement. Due to the low maximum speed, the air resistance becomes negligible, but the losses in the brakes will become more dominant.

In this blog post, I’ll focus on the power consumption when traveling long distance on the freeway, without much traffic. It’s the easiest way to get a ball park figure and it’s also a relevant situation for those who only use their maximum battery capacity when making long trips. We start with the most simplistic situation, which will be the absolute best case for efficiency that can be achieved. It is based on the following starting points:

• Constant speed of 100 km/h (62 mph)
• No wind
• No traffic
• No changes in altitude

Let’s start with the most interesting; for those who are impatient.

Air resistance

The air resistance is determined by the following parameters:

• Drag coefficient (Cw value)
• Frontal surface area
• Air density
• Air speed (wind)
• Driving speed

Drag coefficient (Cd value)

The drag coefficient defines how aerodynamic an object is. It is determined by the skin friction and the form drag. Less aerodynamic shapes and materials create a lot of turbulence, which means that the air gets subjected to chaotic changes in pressure, flow velocity and direction. This state requires a lot of power, which is subtracted from the kinetic energy of the vehicle, causing it to slow down unless more power is added on the drive side.

Below is a picture of some basic shapes and their impact on the drag coefficient.

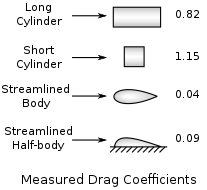
As you might expect, a rectangular box like a big truck will have a much higher drag coefficient than something shaped like what we associate with the shape of a waterdrop. Fun fact: Did you know a waterdrop actually doesn’t take this shape when falling? Off-topic, but if you’re interested, see this video.

Taking aerodynamics into account in designing a vehicle is not new. Compare the shape of a Model T Ford with this 1914 A.L.F.A. 40/60 HP Aerodinamica Prototype and you can see that we’ve known for over a 100 years, that the shape plays a big role in achieving efficiency. This prototype could attain a top speed of 86 mph from its 70 horsepower engine. Not bad for such a large vehicle!

So why don’t all modern cars have a waterdrop shape? The simple answer is: practicality. The optimal shape for aerodynamics doesn’t lead to the optimal shape for passenger space. So to create the same inside space, you need to use more material and manufacturing all these curved shapes is more complex and thus more expensive than making box shaped cars.

It’s not just the main shape that has a big effect on the drag coefficient. It’s also a lot of smaller effects that can play a big role. For instance mud flaps, turbulence around the wheels, big gaps between parts, spoilers etc. all have a negative effect by disturbing the air flow. You might not expect it, but a modern day BMW 3-series actually has a significantly lower drag coefficient than a Porsche 997 turbo (0.23 vs 0.31). See this Wikipedia page for a large list of car models and their coefficient of drag.

Aptera’s real competition comes from EV’s like the Tesla Model 3, which has a drag coefficient of 0.23. And Aptera? It’s said to have a drag coefficient of 0.13. Much better than any car that has ever been produced in serious numbers. To achieve this Aptera has had to change it shape radically with respect to more mainstream cars. Most notably by creating a shape that converges to a thin line in the back, by opting for only 3 wheels instead of 4 and by setting the two front wheels apart from the main body.

Next, let’s talk about the second determining factor in designing a car to achieve low aerodynamic drag: frontal surface area.

Frontal surface area

As you might understand, the smaller the frontal surface of the car, the less air needs to be pushed away to force the car through the air. If a child and an adult stick their arm out the window, the shape of their hand and thus the drag coefficient will be similar, but the force on the child’s hand will be much lower than the force on the hand of the adult.

Unfortunately Aptera hasn’t published the frontal surface area. I have however found to sources for the product of Cd and A. In this online calculator it lists the Aptera 3 (the current design) with a Cd*A of 0.27 m², or 2.94 ft². Assuming the Cd = 0.13 was correct, this would indicate an effective frontal surface of 2.1 m² or 22.6 ft².

In comparison, according to the same calculator, a Tesla model 3 has a Cd*A of 0.51 m² or 5.50 ft². This would mean Aptera would be almost twice as efficient as a Tesla model 3. This is actually less impressive than I expected based on their earlier statements in a video, where “3x more efficient than a small electric car” is mentioned, while showing a picture of a Tesla model 3. Also, this source shows a significantly lower Cd*A for the Aptera 2 series (2019) of 0.19 m².

I’ve asked Aptera for the numbers of Cd and A. Until I’ve got an exact answer, let’s assume the only source I have for the current model is correct. We’ll calculate with 2.1 m² or 22.6 ft².

Power needed at 100 km/h or 62 mph

The power necessary to overcome the drag is defined as follows:

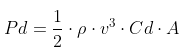
With:

• Pd = power in Watts
• ρ = density of the air in kg/m³
• v = speed in m/s
• Cd = coefficient of drag (unitless)
• A = the frontal surface area in m²

According to this source, at IUPAC standard temperature and pressure (0 °C and 100 kPa), dry air has a density of 1.2754 kg/m³. With the earlier mentioned assumptions of no wind and driving speeds of 100 km/h, this leads to the following power for overcoming drag:

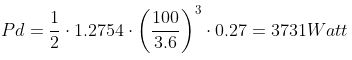
Let’s use this power to calculate the energy per unit of distance (Wh/km or Wh/mile), that’s commonly used. If the Aptera uses 3731 Watt, for an hour, driving 100 km/h, it will have used 3.69 kWh over a distance of 100 km or 62 miles. This breaks down to only 37 Wh per km, or 60 Wh per mile.

Note that the efficiency decreases at larger speeds, since the drag force increases quadratic with speed. So when traveling say 150 km/h (91 mph), the energy to overcome drag more than doubles to 84 Wh per km, or 135 Wh per mile.

Now that we have a ball park figure (under ideal circumstances and with some uncertainty in the inputs) let’s take a look at the other losses that are occurring at 100 km/h.

Rolling resistance

Rolling resistance is mainly caused by the non-elastic effects, meaning those deformations that don’t give back all their energy when pressure is removed. This includes hysteresis in the tires and in the road surface, permanent plastic deformation (for instance when driving over a dirt road). Another effect is the slippage that occurs between the tire and the road, which dissipates energy. The rolling resistance depends on several factors such as:

• Wheel diameter
• Width of the wheel
• Load on the wheel
• Type of surface (concrete, asphalt, dirt roads etc.)

The rolling resistance coefficient (Crr) of a typical car tire on asphalt is about 0.01. Aptera doesn’t plan to use special tires. Special tires are usually more expensive, have lower availability and could compromise on grip. Here’s a list of tires with low rolling resistance, to get an idea how much could be gained theoretically.

The force to push the car to overcome rolling resistance is defined as:

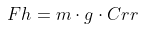
The vertical force is caused by gravity. The weight of the Aptera depends on the chosen battery pack. According to the Aptera FAQ, the vehicle weighs 1800 lbs.-2,200 lbs. Let’s calculate with the median value of 2000 lbs., or 907 kg. Using the Crr of 0.01 this results in:

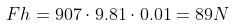
This means you could basically let your 8 year old son push you to the side of the road if you ever run out of battery. Convenient, right?

Now, we need to calculate what this means for the energy consumption per km and mile. For this we use the simple equation of work, which dictates that the amount of energy needed to overcome a force over a certain distance is the product between the force and the distance. This results in the following:

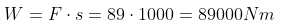
Since we’ve been using Wh and kWh as units of measure, let’s transfer this result in those units, by multiplying by 2.778*10^-7. This results in 24.7 Wh/km or 39.8 Wh/mile.

Note that the energy needed to overcome the rolling resistance isn’t actually influenced by the number of wheels or the driving speed. In reality there will be some small effects on the exact rolling resistance when for instance a tire heats up (high speed driving) and there would probably be minor differences between pushing a 1000 kg car with 3 wheels instead of 4. The logic is however, that if you use more wheels, you decrease the force per wheel, but you increase the number of wheels that need to be moved. No big differences are to be expected between a vehicle with 4 or 3 wheels.

Mechanical drivetrain losses

Because Aptera uses in wheel motors, it gets rid of mechanical losses in the drivetrain entirely. There are no drive shafts or differentials. The only mechanical losses that occur are in the wheel bearings, in the steering and in the suspension. Since these losses are relatively low when driving on a proper highway, let’s neglect these losses for now.

Friction losses when applying the brakes

When you let a vehicle slow down by applying the brakes, all kinetic energy gets turned into waste heat. Of course this is a nightmare when considering efficiency. That’s why electric vehicles try to save as much of the kinetic energy as possible by using regenerative braking. Regenerative braking means you use the motors as generators and charge the battery packs while slowing down.

For our 100 km/h constant speed use case, we’re not interested in these losses, but let’s get a ball park figure anyway on how much energy is lost when slowing down.

Let’s assume a medium traffic situation in which half of the energy is saved by using regenerative braking and the other half gets lost in heating up the brakes. Kinetic energy is defined as:

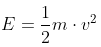
So, when we would slow down from 50 km/h (31 mph) to a full stop and lose 50% of all energy, we’re wasting 0,012 kWh. Since kinetic energy is squared with speed, slowing down from 100 km/h (62 mph) with 50% regeneration leads to losses 4 times as high. Assuming the 100Wh/mile advertised by Aptera, this means that having to stop from 100 km/h with 50% regenerative braking costs as much as half a mile of driving.

Auxiliary equipment

When driving, some electrical consumption will be present which is unrelated to the drive of the vehicle. Things like the screen on the center console, the hardware that operates it, the stereo system, charging your phone etcetera. Let’s assume all these systems are design efficiently and consume a combined 100 W of power. At speeds of 100 km/h, it would use 100 Wh per 100 km, or 1 Wh per km. Interestingly, this number drops with increasing speed. This is because you use them for a shorter time over the same distance. So, hit that throttle to get this number down ;-).

Note that the power consumption of the auxiliary equipment skyrockets when things like heating and airconditioning are activated. Aptera is aware of this and is still figuring out how to find ways to avoid having to use highly inefficient, but simple and cheap, solutions like resistive heating. A heat pump, heated seats etc. could be solutions to minimize the negative impact of climate control. For this calculation, I will assume 100 W of power for heating. It’s an assumption with a very high level of uncertainty. I’ve based it on a heated seat on high (45W) plus some ventilation with resistive heating. So, this is another 1 Wh per km.

Electrical losses

When taking the electricity from the battery pack and transforming it to the physical rotation of the wheels, electrical losses occur. The battery pack, cables and motors all have electrical resistance which leads to losses when the needed currents are drawn. According to this aforementioned Aptera video, electrical efficiency is higher than 90% for the selected components.

Now, let’s take the mechanical losses for our best case highway driving situation and see where we are in terms of efficiency.

Conclusion: efficiency at constant speed

So, now that we have all losses defined, let’s get it all down to one number for driving at a constant speed of 100 km/h. First, we add up the energy to overcome air resistance (37.3 Wh/km) and rolling resistance (24.7 Wh/km) and divide this by the efficiency of the electric drive.

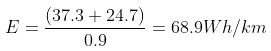
When adding the assumed power consumption of the auxiliary systems and climate control, we get to total efficiency at 100 km/h of 70.9 Wh/km, or 114.15 Wh/mile.

This is higher than the 100W/mile reported by Aptera, even though some best case assumptions (no braking, no wind, no rain, low power consumption for climate control etc.) were made. I think this could be mainly caused by one or two things:

• 100 km/h constant driving is actually more worst case than the EPA driving cycle
• The numbers I’ve found for the Cd*A were not correct
• I’ve made a mistake (Trust me, I’m an engineer! But, if you find a mistake, please let me know)

Below, two graphs, one for metric and one for imperial units, show the energy consumption at constant speed, based on the calculations in this blog post. On the horizontal axis the constant speed of driving is used as an input. On the vertical axis, the resulting energy consumption is given.

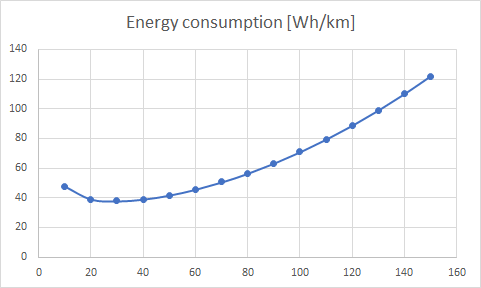
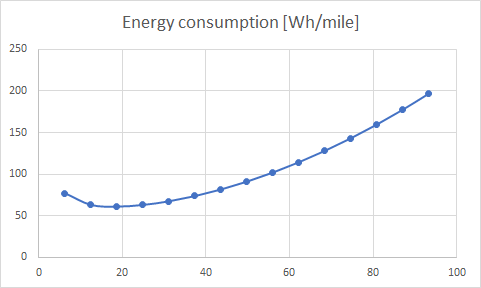
Thanks for reading. I hope you found this analysis informative. If you have any remarks, please feel free to leave a remark in the comment section. It would also be very helpful if you’d use my referral link when you decide you want to order an Aptera. On my page about ordering, I list a few reasons why I would recommend it.